Factorization Machines & Online Optimization
Outline
- Online Optimization
- TG
- FOBOS
- RDA
- FTRL
- Factorization Machines
- Model
- Training
Outline Learning
- Online Learning 是工业界比较常用的机器学习算法,在很多场景下都能有很好的效果。
- Online Learning 能够根据线上反馈数据,实时快速地进行模型调整,使得模型及时反映线
上的变化,提高线上预测的准确率。 Batch Learning vs. Online Learning
Batch Learning 更新模型的周期较长,
Online Learning 能够实时更新模型。
Batch Learning 对硬件资源要求高,
Online Learning 对硬件资源要求低。
Batch Learning 假设样本服从 IID 分布,
Online Learning 对样本分布无要求。

最优化问题
- 通常最优化问题可以形式化地表示为:
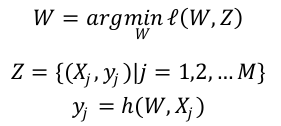
- 其中, Z是观测样本集合(训练集),
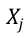 是第 j 个样本的特征向量,
是第 j 个样本的特征向量,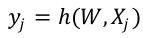 是第j个样本的预测值。
是第j个样本的预测值。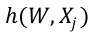 是特征向量到预测值的映射函数。
是特征向量到预测值的映射函数。 是最优化求解的目标函数,即损失函数,通常表示为为各个样本损失函数的累加,即
是最优化求解的目标函数,即损失函数,通常表示为为各个样本损失函数的累加,即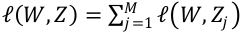 。W是特征权重,也就是需要求解的参数。
。W是特征权重,也就是需要求解的参数。
Batch/Stochastic Gradient Descent


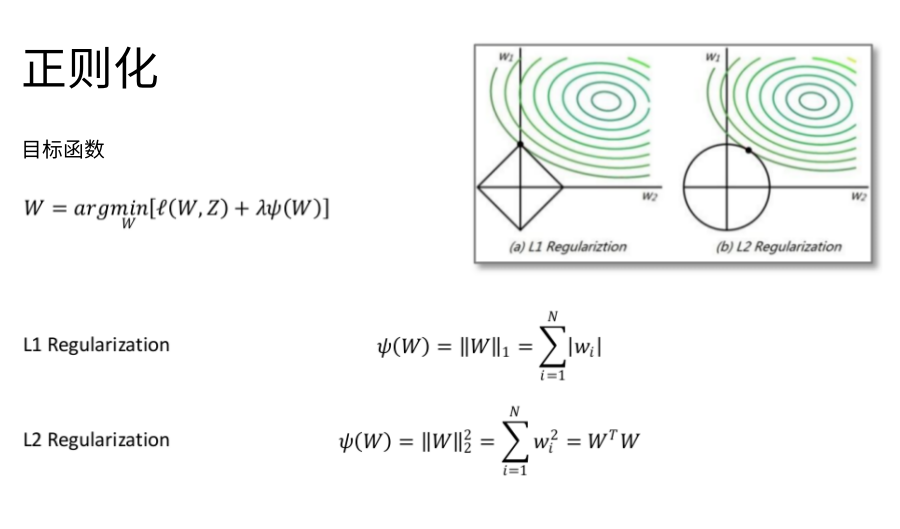
模型稀疏性的好处
- 特征选择,易于解释
- 减少模型预测的时间复杂度,降低存储模型的空间占用
- 更加符合奥卡姆剃刀原理
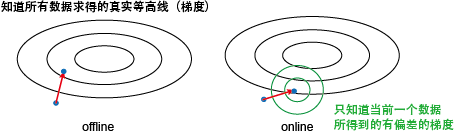
如何在 Online Learning 中得到稀疏模型?
- 简单截断法
- 截断梯度法(TG)
- FOBOS算法
- RDA算法
- FTRL算法
简单截断法
- 以k为窗口,当t/k不为整数时采用标准的SGD进行迭代,当t/k为整数时,采用如下权重更新方式:
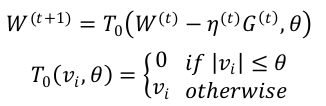
- 这种方法实现起来很简单 , 也容易理解。但实际中 ( 尤其在 OGD 里面 )W 的某个系数比较小可能是因为该维度训练不足引起的,简单进行截断会造成这部分特征的丢失。
梯度截断法(TG)
- TG 同样是以 k 为窗口,每 k 步进行一次截断。当 t/k 不为整数时 λ (t) = 0 ,当 t/k 为整数时 λ (t) = kλ 。从下面公式可以看出, λ 和 θ 决定了 W 的稀疏程度,这两个值越大,则稀疏性越强。尤其令 λ = θ 时 , 只需要通过调节一个参数就能控制稀疏性。
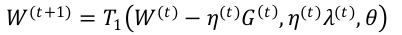
简单截断法和梯度截断法比较
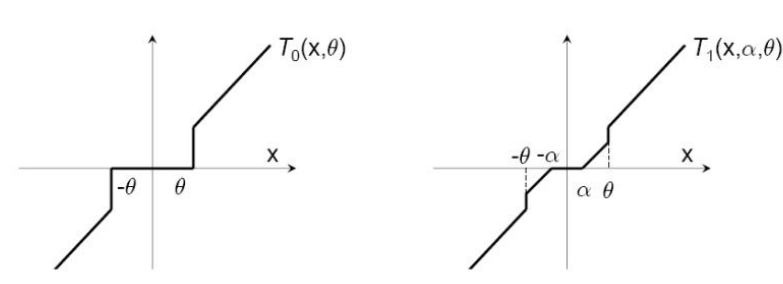
FOBOS算法
在 FOBOS 算法中,权重的更新分为两步:
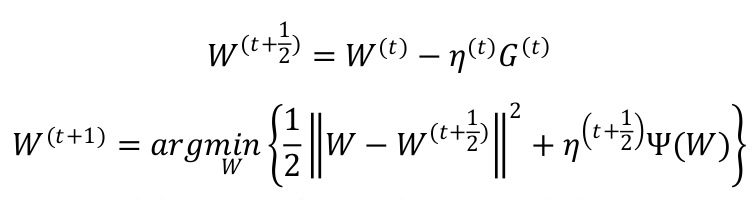
前一个步骤实际上是一个标准的梯度下降步骤,后一个步骤可以理解为对梯度下降的结果进行微调。
观察第二个步骤,发现对 W 的微调也分为两部分 :
(1) 前一部分保证微调发生在梯度下降结果的附近 ;
(2) 后一部分则用于处理正则化,产生稀疏性。
L1-FOBOS 算法
在L1的正则化下,有 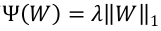 。为简化,用向量
。为简化,用向量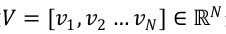 来表示
来表示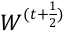 。用标量
。用标量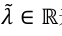 来表示
来表示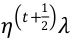 。因此,可得,
。因此,可得,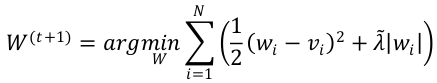
由于求和公式的每一项都大于等于零,所以可以按每一维度单独求解,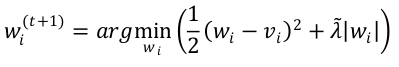
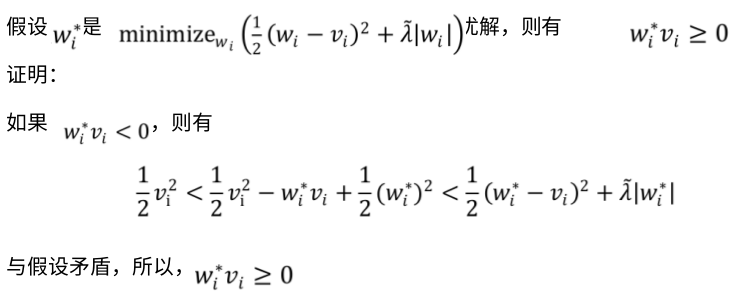


RDA
在 RDA 中,权重的更新策略是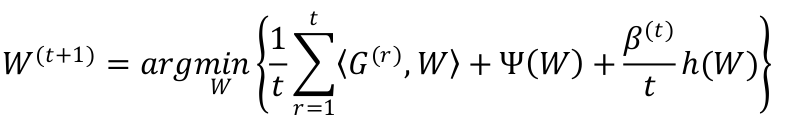
其中,线性项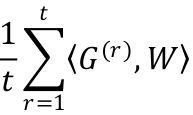 包含之前所有梯度与 W 乘积的平均值,正则项
包含之前所有梯度与 W 乘积的平均值,正则项 额外正则项
额外正则项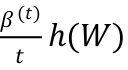 ,
,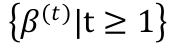 是一个非负且非递减序列, h(W) 是一个辅助的严格凸函数。
是一个非负且非递减序列, h(W) 是一个辅助的严格凸函数。
L1—RDA

- 在 L1-FOBOS 中,截断的判定条件是

通常,定义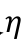 为与
为与 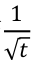 正相关的函数。因此, L1-FOBOS 的截断阈值是,随着 t 的增加,这个阈值会逐渐降低。而, L1-RDA 中的截断阈值是一个常数,不随着 t 的变化而变化。因此,可以认为 L1-RDA 比 L1-FOBOS 在截断判定上更加 aggressive ,也就是说,更容易产生稀疏性。
正相关的函数。因此, L1-FOBOS 的截断阈值是,随着 t 的增加,这个阈值会逐渐降低。而, L1-RDA 中的截断阈值是一个常数,不随着 t 的变化而变化。因此,可以认为 L1-RDA 比 L1-FOBOS 在截断判定上更加 aggressive ,也就是说,更容易产生稀疏性。 - 不同于 TG 和 L1-FOBOS 仅采用单次梯度对权重进行更新, L1-RDA 公式中包含了梯度的累加平均值,因此,可以避免某些维度由于训练不足导致被截断的问题,在精度和稀疏性上的表现更加均衡。
FTRL
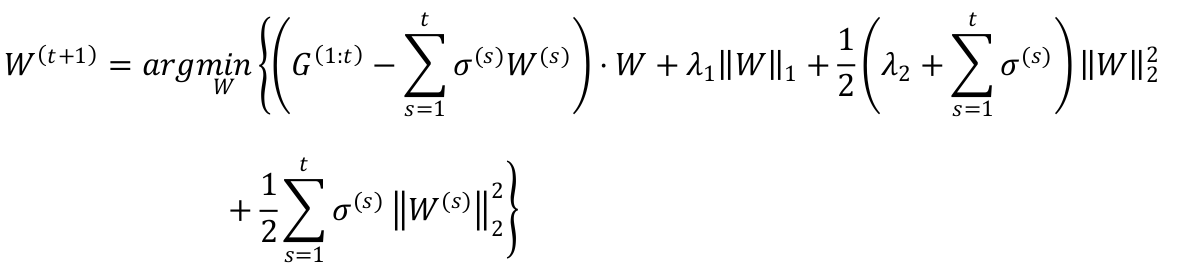


Per-Coordinate Learning Rate
在 FTRL 中,每一个维度上的学习率是单独考虑的:如果特征 1 比特征 2 变化的快,那么特
征 1 上的学习率应该下降的更快。

其中, α 和 β 是需要人为指定的超参数。
Factorization Machines
在现实世界中,许多应用问题(如文本分析,推荐系统等)会产生高度稀疏的(特征)数据
,即特征向量中大多数的分量都为 0 。这里,我们以电影评分系统为例。
考虑电影评分系统中的数据,它的每一条记录都包含了用户 u∈U 在什么时候 t∈R 对哪部电
影 i∈I 打了多少分 r∈{1, 2, 3, 4, 5} 。
模型方程
- 线性回归
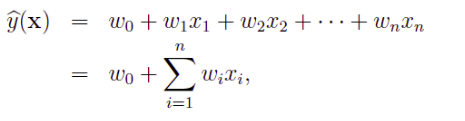
- 引入特征之间的关系( interaction )
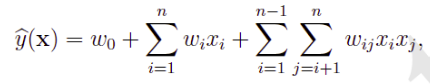
- 引入辅助向量
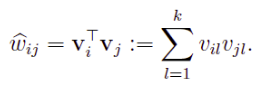
特征交叉( Feature Cross )
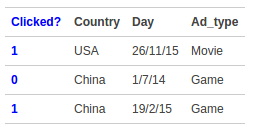
线性模型无法学习到特征之间的相关性。例如,特征“ Country=USA” 与特征 “Day=26/11/15” ,
特征“ Country=China” 与特征 “Day=19/2/15” 这样的关联特征,对用户的点击有着正面的影响。
实际问题中,还存在“化妆品”特征与“女性”特征,“球类运动配件”特征与“男性”特征等等。

学习算法
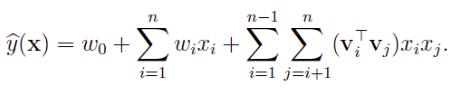
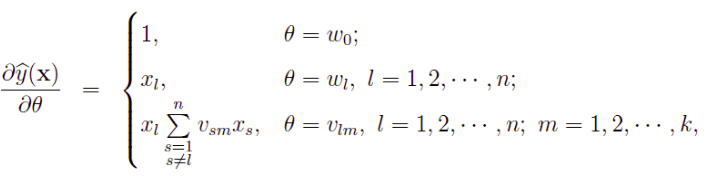
最优化问题

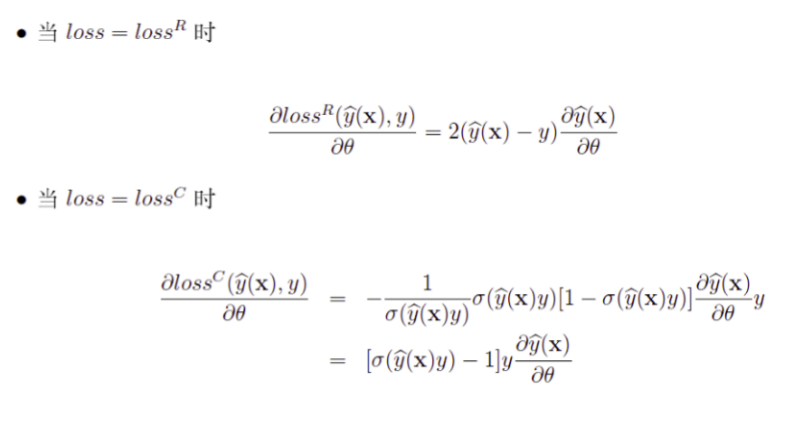
随机梯度下降法
