时间序列分析
Knowledge sharing by FC
1 基本概念
1.1 随机过程
设 $X_0, X_1,X_2…$ 是一列独立同分布的随机变量序列,令
$$
S_n = S_0+X_1+X_2+…+X_n
$$
则随机变量序列 $$S_n$$ 为随机过程。
1.2 均值/协方差/方差函数
对于序列${X_t}$:
均值函数:
$$
\mu_X(t)=E[X(t)]
$$
协方差函数:
$$
\gamma_X(s,t)=E[(X(s)-\mu_X(s))(X(t)-\mu_X(t))]
$$
方差函数:
$$
D_X(t)=r_X(t,t)=E[(X(s)-\mu_X(s))^2]
$$
Note:
为弱平稳的描述做准备。
1.3 平稳性
平稳性:时间序列的行为不随时间改变。
Why stationary?
简化问题的假设。
- 强平稳:对于一个时间序列${Zt}$与任意整数k,如果
$$
Z\{t1}, Z_{t2},…,Z_{tn}
$$
与
$$
Z_{t1-k}, Z_{t2-k},…,Z_{tn-k}
$$
的联合分布一致,那么称该序列强平稳。 - 弱平稳:对于一个序列,若其均值函数是常数,协方差函数仅与时间差相关,那么称该序列弱平稳。
Note:
强弱平稳并不相互包含。满足假设则预测结果好。ADF检验等,对不平稳的序列可做差分。
1.4 差分方程
一阶差分方程:
一个变量在$t$时刻的值记作$y_t$,$t$时刻和$t-1$时刻的值可以由以下一阶线性差分方程刻画:
$$
y_t=\phi y_{t-1+w_t}
$$
差分方程表达一个变量与他前期值的关系。
p阶差分方程
$$
y_t=\phi_ty_{t-1}+\phi_2y_{t-2}+…+\phi_py_{t-p}+w_t
$$
差分方程的递归解
$$
y_t=\phi^{t+1}y_{-1}+(w_t+\phi w_{t-1}+\phi^2w_{t-2}+…+\phi^{t-1}w_1+\phi^tw_0)
$$
动态乘子
$$
\frac{\partial y_t}{\partial w_0}=\phi^t,\frac{\partial y_{t+j}}{\partial w_t}=\phi^j
$$
Note:
描述t时刻的扰动wt对于j时刻后的影响。
phi的取值以1为界对于过程的影响(消散,放大)
1.5 延迟算子
令B为一步延迟算子,如果当前序列乘以一个延迟算子,表示把当前序列值的时间向过去拨一个时刻。
使用延迟算子表示的一阶差分方程:
$$
y_t=\phi y_{t-1}+w_t\\
y_t=\phi By_t+w_t\\
(1-\phi B)y_t=w_t
$$
延迟算子性质
$$
\begin{align}
BX_t&=X_{t-1}\\
B^2X_t&=X_{t-2}\\
&…\\
B^nX_t&=X_{t-n}\\
\end{align}
$$
$$
\begin{align}
&(1)B^0=1\\
&(2)若c为任意常数,则B(cX_t)=cB(X_t)=cX_{t-1}\\
&(3)(1-B)^n=\sum_{i=0}^n \frac{(-1)^n n!}{i!(n-i)!}B^i
\end{align}
$$
2 线性平稳时间序列
2.1 自回归过程(AR)
一阶自回归过程AR(1):
如${X_t}$为平稳序列,且满足如下差分方程:
$$
X_t=c+\phi X_{t-1}+\varepsilon_t
$$
其中系数表示对前一项的依赖程度,扰动为白噪声序列,则称${X_t}$满足一阶自回归模型。
Note:
WN: mean=0 方差sigma,不少分析中会先把序列中心化,即减均值。认为序列与前期值有关。
平稳条件:
特征方程:$\lambda-\phi=0$的根的绝对值小于1,即
$$
|\phi|<1
$$
Note:
这与差分方程中动态乘子的意义一致。
方差与均值
$$
E(X_t)=\frac{c}{1-\phi}\\
E(X_t-\mu)^2=\frac{\sigma^2}{1-\phi^2}
$$
利用延迟算子,一阶自回归模型可以表示为:
$$
(1-\phi B)X_t=c+\varepsilon_t\\
\begin{align}
X_t&=(1-\phi B)^{-1}(c+\varepsilon_t)\\
&=\frac{c}{1-\phi}+(1-\phi B)^{-1}\varepsilon_t
\end{align}
$$
如果满足平稳条件,则可表示为:
$$
\begin{align}
X_t&=\frac{c}{1-\phi}+(1+\phi B+…+\phi^j B^j+…)\varepsilon_t\\
&=\frac{c}{1-\phi}+\varepsilon_t+\phi\varepsilon_{t-1}+…+\phi^j\epsilon_{t-j}…
\end{align}
$$
Note:
类似于一个数列极限。平稳则扰动项必须收敛,否则与影响无限扩大。AR1是一个无限阶的移动平均过程。
2.2 移动平均过程
一阶移动平均过程MA(1):
${X_t}$若满足如下方程:
$$
X_t=\mu+\varepsilon_t-\theta\varepsilon_{t-1}
$$
其中$\mu$为常数,$\theta$为移动平均系数,$\varepsilon$为白噪声过程,则称${X_t}$满足一阶移动平均模型。
Note:
认为序列和前一时刻的扰动有关。
MA(1)的均值与方差
$$
E(X_t)=\mu
$$
$$
E(X_t-\mu)^2=E(\varepsilon_t-\theta\varepsilon_{t-1})^2=(1+\theta^2)\sigma^2
$$
2.3 自回归移动平均过程
ARMA(p,q)模型的一般表达式为:
$$
X_t=c+\phi_1 X_{t-1}+…+\phi_p X_{t-p}+\\
\varepsilon_t-\theta_1\varepsilon_{t-1}-…-\theta_q\varepsilon_{t-q}\\
\forall s<t, E(X_s\varepsilon_t)=0
$$
2.4 相关系数
2.4.1 自相关系数ACF
AR(1)的自协方差与自相关系数:
$$
\gamma_k=E(x_tx_{t-k})=\phi_1E(x_{t-1}x_{t-k})+E(\varepsilon_tx_{t-k})=\phi_1\gamma_{k-1}\\
\gamma_k=\phi_1^k\gamma_0
$$
$$
\rho_k=\frac{\gamma_k}{\gamma_0}=\phi_1^k
$$
Note:
这里是中心化后的序列,自协方差受幅度影响,相关系数去除幅度影响。
AR(p)的自协方差与自相关系数:
$$
\gamma_k=\phi_1\gamma_{k-1}+…+\phi_p\gamma_{k-p}, k>0\\
\rho_k=\phi_1\rho_{k-1}+…+\phi_p\rho_{k-p}, k>0
$$
(Yule-Walker方程,系数阵正定,可解回归系数)
Note:
p1=1,自己和自己的相关系数。模型定阶后可以求p阶协方差,解方程组。
MA(1)的自协方差与自相关系数:
$$
\gamma=E(x_t-\mu)(x_{t-k}-\mu)=E(\varepsilon-\theta\varepsilon_{t-1})(\varepsilon_{t-k}-\theta\varepsilon_{t-k-1})\\
\gamma_0=(1+\theta^2)\sigma^2\\
\gamma_1=\theta\sigma^2\\
\gamma_k=0,k>1\\
\rho_1=\frac{\theta\sigma^2}{(1+\theta^2)\sigma^2}=\frac{\theta}{1+\theta^2}
$$
高阶自相关系数均为0。
MA(q)的自协方差与自相关系数:
$$
\gamma_j=(\theta_j+\theta_{j+1}\theta_1+\theta_{j+2}\theta_2+…+\theta_q\theta_{q-j})\sigma^2, j=1,2,…,q\\
\rho_j=\frac{\theta_j+\theta_1\theta_{j+1}+…+\theta_{q-j}\theta_{q}}{1+\theta_1^2+…+\theta_q^2}, j=1,2,…,q
$$
解非线性方程,可得滑动平均系数。
Note:
for j>q, gamma=0,p=0,解非线性方程,可得滑动平均系数
ARMA(p,q)的自协方差与自相关系数:
$$
X_t=c+\phi_1 X_{t-1}+…+\phi_p X_{t-p}+\\
\varepsilon_t-\theta_1\varepsilon_{t-1}-…-\theta_q\varepsilon_{t-q}
$$
先同乘以$X_{t-k}$,求均值得自协方差,得到Yule-Walker方程,求回归系数,然后构造:
$$
X_t^*=X_t-(\phi_1 X_{t-1}-…-\phi_p X_{t-p})
$$
$X_t^*$为MA(q)序列,按MA(q)序列计算自协方差/自相关系数,解非线性方程得滑动回归系数。
2.4 相关系数
2.4.2 偏自相关系数PACF
$$
\begin{align}
\varphi_{11}&=\rho_1\\
\varphi_{k+1,k+1}&=(\rho_{k+1}-\sum_{j=1}^k\rho_{k+1-j}\varphi_{k,j})(1-\sum_{j=1}^k\rho_j\varphi_{k,j})\\
\varphi_{k+1,j}&=\varphi_{k,j}-\varphi_{k+1,k+1}\varphi_{k+1,k+1-j}, j=1,2,…k
\end{align}
$$
Note:
用于定阶。
$$
D=
\begin{vmatrix}
1 & \rho_1 & \cdots & \rho_{k-1}\\
\rho_1 & 1 & \cdots & \rho_{k-2}\\
\vdots & \vdots & &\vdots\\
\rho_{k-1} & \rho_{k-2} & \cdots & 1\\
\end{vmatrix}
$$
$$
D_k=
\begin{vmatrix}
1 & \rho_1 & \cdots & \rho_{k-1}\\
\rho_1 & 1 & \cdots & \rho_{k-2}\\
\vdots & \vdots & &\vdots\\
\rho_{k-1} & \rho_{k-2} & \cdots & \rho_k\\
\end{vmatrix}
$$
$$
\varphi_{kk}=\frac{D_k}{D}
$$
3 实际应用
3.1 模型(阶数)识别
ACF/PACF定阶
| 序列 | AR(p) | MA(q) | ARMA(p,q) |
|---|---|---|---|
| ACF | 拖尾 | q阶截尾 | 拖尾 |
| PACF | p阶截尾 | 拖尾 | 拖尾 |
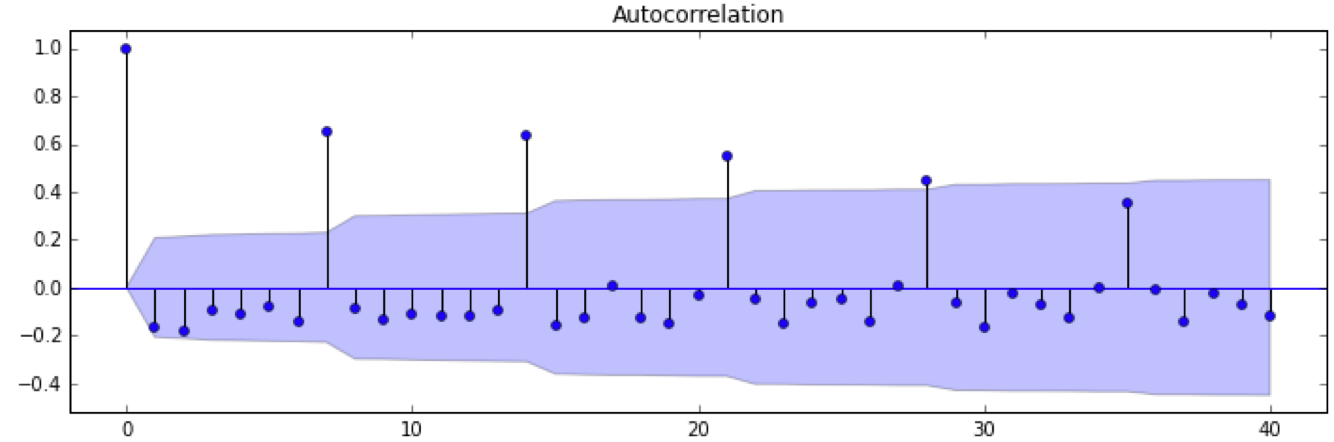
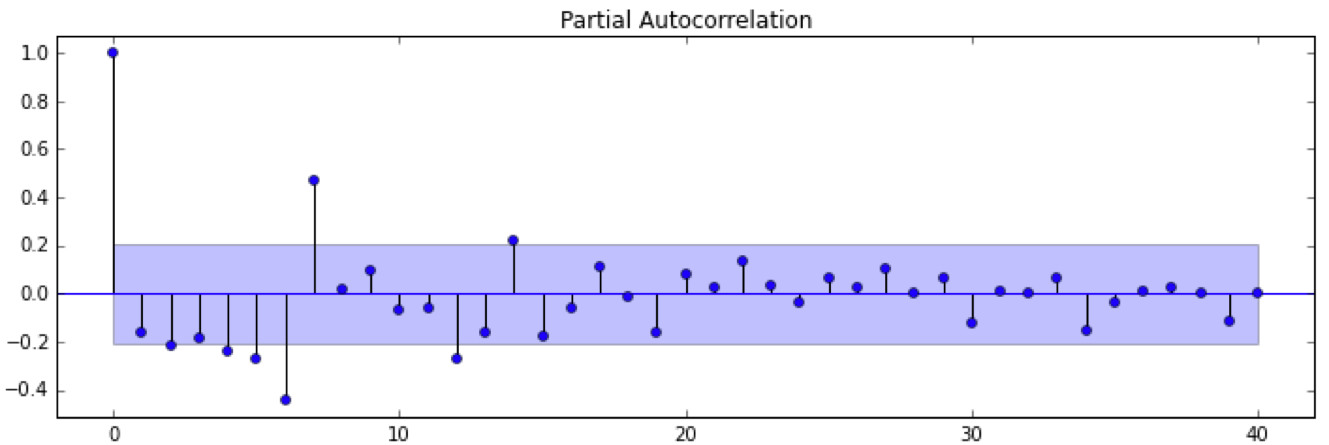
AIC/BIC准则:
$$
AIC(p,q)=ln\hat\sigma_k^2+\frac{2(p+q+1)}{N}\\
BIC(p,q)=log\hat\sigma_k^2+\frac{p+q+1}{N}logN
$$
选择最大阶数($N^\frac{1}{2},logN,\frac{N}{10}$),
计算使AIC or BIC最小的p,q,作为模型阶数。
Note:
耗时,每次要计算出模型,再计算拟合残差,MAXLAG^2次计算。
3.2 参数估计
- 矩估计
- 极大似然估计
Note:
矩估计:Yuler-Walker方程等。
极大似然估计
以AR(1)为例:
$$
X_t=c+\phi X_{t-1}+\varepsilon_t
$$
序列观测值:$x_1,…x_T$
$\varepsilon_t$为白噪声,参数为$\theta=(\phi, \sigma^2)$
对于第一个样本,$X_1:N(\frac{c}{1-\phi},\frac{\sigma^2}{1-\phi^2})$,即$X1$的概率分布:
$$
f\{X_1}(x_1;\phi,\sigma^2)=\frac{1}{\sqrt{2\pi}\sqrt{\sigma^2/(1-\phi^2)}}exp[-\frac{x_1^2}{2\sigma^2/(1-\phi^2)}]
$$
Note:
假设X1的期望与方差,与2.3中分析的一致。如果认为初始值也服从N(0,\sigma^2),则忽略了初始值之前的影响。
考察,第二个样本$X_2$在$X_1=x_1$已知条件下的概率分布,由于
$$
X_2=c+\phi X_1+\varepsilon_2
$$
$$
f_{X_2|X_1}(x_2|x_1;\phi,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}exp[-\frac{(x_2-\phi x_1)^2}{2\sigma^2}]
$$
根据贝叶斯公式,$X_1,X2$的联合分布为:
$$
f\{X_1,X_2}(x_1,x_2;\phi,\sigma^2)=f_{X_1}(x_1;\phi,\sigma^2)f_{X_2|X_1}(x_2|x_1;\phi,\sigma^2)
$$
Note:
X2~N((c+\phi x_1), \sigma^2)。常数+\varepsilon_t。
在前t-1个值已知的条件下,实际上$Xt$仅与$X{t-1}$有关:
$$
f_{X_t|X_{t-1},…,X_1}(x_t|x_{t-1},…,x_1;\phi,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}exp[-\frac{(x_t-\phi x_{t-1})^2}{2\sigma^2}]
$$
则$X_T…X1$的联合分布为:
$$
f\{X_T,…,X_1}(x_T,…,x_1;\phi,\sigma^2)=f_{X_1}(x_1;\phi,\sigma^2)\prod_{t=2}^{T}f_{X_t|X_{t-1}}(x_t|x_{t-1};\phi,\sigma^2)
$$
对数似然函数为:
$$
L(\phi,\sigma^2)=-\frac{T}{2}log(2\pi)-\frac{1}{2}log[\sigma^2/(1-\phi^2)]-\frac{1}{2\sigma^2/(1-\sigma^2)}x_1^2\\
-[(T-1)/2]log(\sigma^2)-\frac{1}{2\sigma^2}\sum_{t=2}^{T}(x_t-\phi x_{t-1})^2
$$
Note:
求偏导数=0的点。
向量形式:
$$
x = (x_1,x_2,…,x_T)^T\\
\Omega=\\
\begin{vmatrix}
E(X_1-\mu)^2 & E(X_1-\mu)(X_2-\mu) & \cdots & E(X_1-\mu)(X_T-\mu)\\
E(X_2-\mu)(X_1-\mu) & E(X_2-\mu)^2 & \cdots & E(X_2-\mu)(X_T-\mu)\\
\vdots & \vdots & &\vdots\\
E(X_T-\mu)(X_1-\mu) & E(X_T-\mu)(X_2-\mu) & \cdots & E(X_T-\mu)^2\\
\end{vmatrix}
$$
$$
\Omega=\sigma^2 V\\
V=\frac{1}{1-\phi^2}
\begin{vmatrix}
1 & \phi & \cdots & \phi^{T-1}\\
\phi & 1 & \cdots & \phi^{T-2}\\
\vdots & \vdots & &\vdots\\
\phi^{T-1} & \phi^{T-2} & \cdots & 1\\
\end{vmatrix}
$$
$$
f_X(x;\phi,\sigma)=(2\pi)^{-T/2}|\Omega^{-1}|^{1/2}exp[-\frac{1}{2}(x-\mu)^t\Omega^{-1}(x-\mu)]
$$
MA(1)的似然函数:
$$
x_t=\mu+\varepsilon_t-\theta\varepsilon_{t-1}\\
L(\theta)=-\frac{T}{2}-\frac{T}{2}log(\sigma^2)-\sum_{t=1}^T\frac{\varepsilon_t^2}{2\sigma^2}
$$
$$
\varepsilon_t=(x_t-\mu)-\theta(x_{t-1}-\mu)+\theta^2(x_{t-2}-\mu)+…+(-1)^t\theta^t\varepsilon_0
$$
Note:
epsilon序列可表示为\theta的函数,非线性函数。
向量形式:
$$
\Omega=\sigma^2
\begin{vmatrix}
(1+\theta^2) & \theta & 0 & \cdots & 0\\
\theta &(1+\theta^2) & \theta & \cdots & 0\\
0 & \theta & (1+\theta^2) & \cdots & 0\\
\vdots & \vdots & \vdots & &\vdots\\
0 & 0 & 0 & \cdots & (1+\theta^2)\\
\end{vmatrix}
$$
$$
f_X(x;\theta)=(2\pi)^{-T/2}|\Omega|^{-1/2}exp[-\frac{1}{2}(x-\mu)^t\Omega^{-1}(x-\mu)]
$$
ARMA(p,q)的极大似然估计:
令$\beta=(\phi_1,…,\phi_p,\theta_1,…,\theta_q)$,
似然函数为:
$$
L(\beta)=-\frac{T}{2}log(2\pi)-\frac{T}{2}log(\sigma^2)-\sum_{t=1}^{T}\frac{\varepsilon_t^2}{2\sigma^2}
$$
$$
\varepsilon_t=x_t-c-\phi_1x_{t-1}-…-\phi_px_{t-p}\\
-\theta_1\varepsilon_{t-1}-…-\theta_q\varepsilon_{t-q}
$$
Note:
参数包含在epsilon序列中
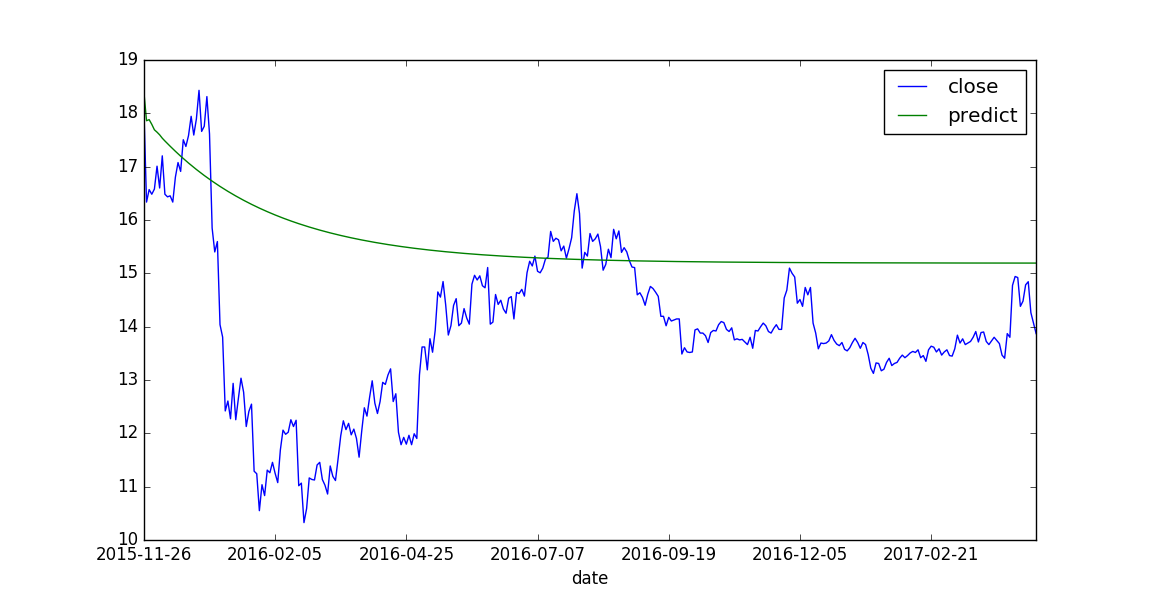
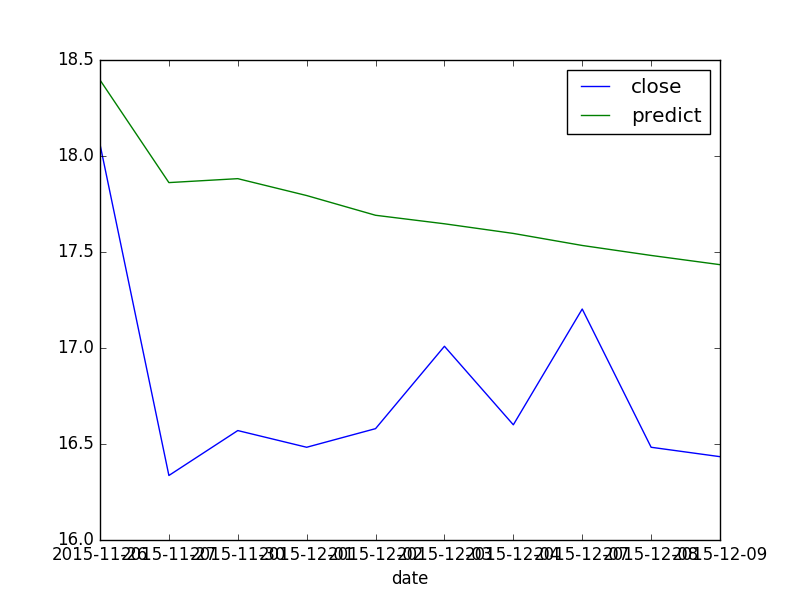
4 一个实验
data:601000.ss, from 2014-8-9 to 2017-4-20,BIC准则定阶,前300个作为训练集,ARMA(4,0)。结果:RMSE:
0.30651974757
MAPE
0.0123583871228
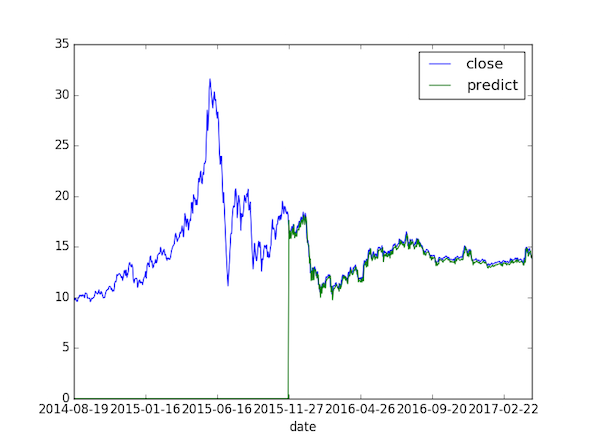
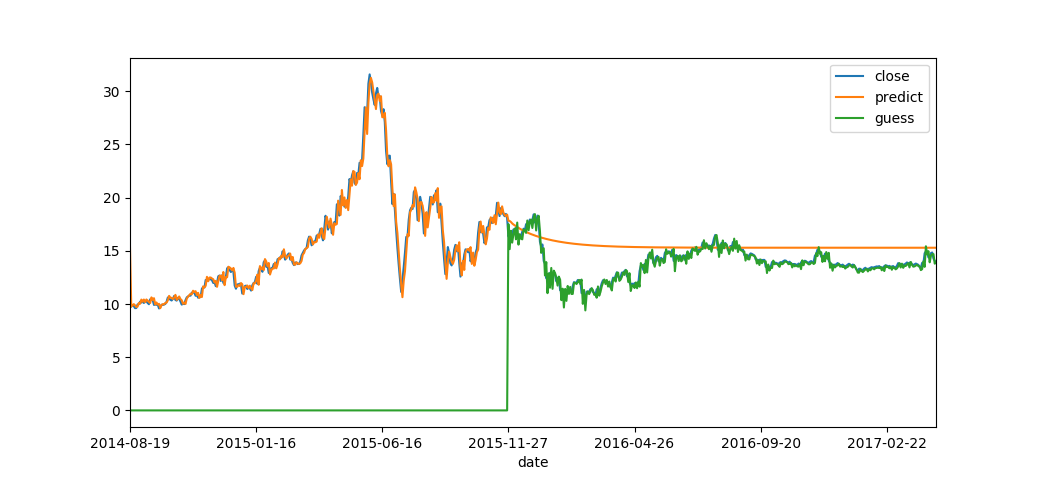
That’s all