Teaching ML

FactorAnalysis

1. Introduction

An extension of principal component analysis(PCA) in the sense of approximating covariance matrix.

Goal

  • To describe the covariance relationships among many variables in terms of a few underlying unobservable random variables, called factors.
  • To reduce dimensions and solve the problem with n<p.

2. Orthogonal Factor Model（正交因子模型）

A Factor Analysis Example

We have a training data $ X_{n \times p} $. Here is its scatter plot. $ y = a $

plot

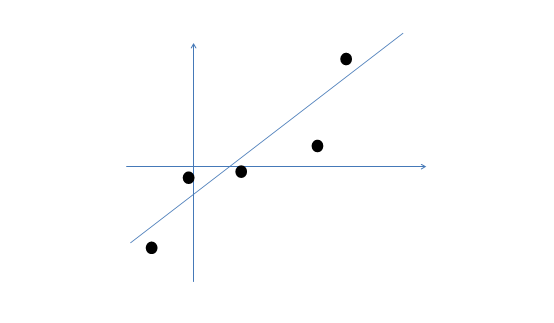
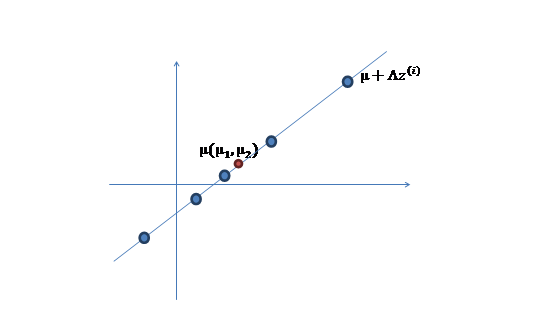
  1. Generate a k dimension variable $F \sim N_k(0,I)$

Factor

  1. There exists a transformation matrix $L \in R^{p \times k}$ which maps F into n dimension space: $LF$

transform

  1. Add a mean $\mu$ on $LF$

add_mu

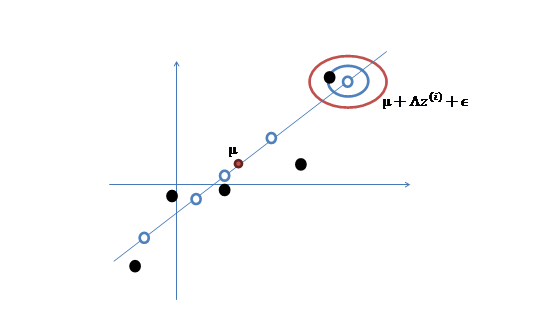
  1. For real instance has errors, add error $\epsilon_{p \times 1}$

$$X = LF+\mu + \epsilon$$

error

Factor Analysis Model

  • Suppose $X \sim \Pi_p(\mu, \Sigma)$
  • The factor model postulates that $X$ is linearly related to a few unobservable random variables $F_1,F_2,…,F_m$, called common factors（共同因子）, through
$$X- \mu = L_{p \times m} F_{m \times 1} + \epsilon_{p \times 1}$$

where $L = (l_{ij})_{p \times m}$ is the matrix of factor loading（因子载荷）, $l_{ij}$ is the loading of variable $i$ on factor $j$, $\epsilon = (\epsilon_1, . . . , \epsilon_p)′$, $\epsilon_i$ are called errors or specific factors（特殊因子）.

  • Assume:

$$E(F) = 0, cov(F) = I_m, $$

$$E(\epsilon) = 0, cov(\epsilon) = \psi_{p \times p} = diag(\varphi_1,.., \varphi_p)$$

$$cov(F, \epsilon) = E(F \epsilon ‘) = 0$$

Then

$$cov(X) = \Sigma_{p \times p} = LL’ + \psi$$

$$cov(X, F) = L_{p \times m}$$

If $cov(F) \ne I_m$, it becomes oblique factor model（斜交因子模型）

  • Define the $i_{th}$ community（变量共同度，或公因子方差）:
$$h_i^2 = \sum_{j = 1}^m l_{ij}^2$$
  • Define the $i_{th}$ specific variance（特殊因子方差）:
$$\varphi_i = \sigma_{ii} - h_i^2$$

Ambiguity of L

  • Let T be any m × m orthogonal matrix. Then, we can express
$$X- \mu = L^*F^* + \epsilon$$

where $L^* = LT$, $F^* = T'F$

  • Since $E(F^*) = 0$ , $cov(F^*) = I_{m}$ , $F^*$ and $L^*$ form another pair of factor and factor loading matrix.
$$ \Sigma = LL' + \psi = L^* L'^{*} + \psi$$ $$h_i^2 = e_i'LL'e_i = e_i'L^*L'^*e_i$$

After rotation, community $h_i^2$ doesn’t change.

3. Estimation

3.1 Principal Component Method

1) Get correlation matrix

$$\hat{Cor}(X) = \Sigma$$

2) Spectral Decompositions

$$\Sigma = \lambda_1\ e_1e_1’\ +\ …\ +\ \lambda_p\ e_pe_p’$$

3) Determine $m$

Rule of thumb: choose $m =\ \# \ of \{\lambda_j>1\}$

4) Estimation

$$\hat L = (\sqrt{\lambda_1}\ e_1,\ …\ ,\ \sqrt{\lambda_m}\ e_m)$$

$$\hat \psi = diag(\Sigma - LL’)$$

$$\hat h_i^2 = \sum_{j = 1}^m \hat l_{ij}^2$$

The contribution to the total sample variance tr(S) from the first common factor is then（公共因子的方差贡献）

$$\hat l^2_{11} + ...+ \hat l^2_{p1} = (\sqrt{\hat \lambda_1}\hat e_1)'(\sqrt{\hat \lambda_1}\hat e_1) = \hat \lambda_1$$

In general, the proportion of total sample variance(after standardization) due to the $j_{th}$ factor = $\frac{\hat \lambda_j}{p}$

3.2 Maximum Likelihood Method

1) Joint distribution:

$$ \begin{bmatrix} f\\ x \end{bmatrix} \sim N \begin{pmatrix} \begin{bmatrix} 0\\ \mu \end{bmatrix}, \begin{bmatrix} I & L'\\ L & LL' + \psi \end{bmatrix} \end{pmatrix}$$

2) Marginal distribution:
$$x \sim N(\mu, LL’+\psi)$$
3) Conditional distribution:
$$\mu_{f|x} = L’(LL’+\psi)^{-1}(x-\mu)$$

$$\Sigma_{f|x} = I - L’(LL’+\psi)^{-1}L$$

4) Log likelihood:

$$l(\mu, L, \psi) = log \prod_{i=1}^n \frac{1}{(2 \pi)^{p/2}|LL’+\psi|} exp \left(-\frac{1}{2}(x^{(i)}-\mu)’(LL’+\psi)^{-1}(x^{(i)}-\mu) \right)$$

EM estimation

  • E Step:
$$Q(f) = \frac{1}{(2 \pi)^{k/2}|\Sigma_{f|x}|} exp \left(-\frac{1}{2}(f-\mu_{f|x})'(\Sigma_{f|x})^{-1}(x^{(i)}-\mu_{f|x}) \right)$$
  • M Step:
$$max\ \ \sum_{i=1}^n \int_{f^{(i)}} Q(f^{(i)})log \frac{p(x^{(i)}，f^{(i)};\mu, L, \psi)}{Q(f^{(i)})} $$
  • Parameter Iteration:

L est

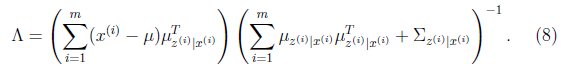
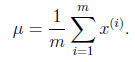
mu est

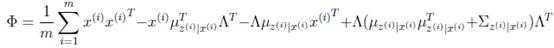
psi est

$$\psi = diag(\Phi)$$

Get more detail on 【机器学习-斯坦福】因子分析（Factor Analysis）

4. Factor Rotation

An orthogonal matrix $T$, and let $L^* = LT$.

  • Goal: to rotate $L$ such that a ‘simple’ structure is achieved.

  • Kaiser (1958)’s varimax criterion（方差最大旋转） :

    • Define $\widetilde l^*_ {ij} = \hat l^*_{ij}/h_i^2$
    • Choose $T$ s.t.
$$max\ \ V=\frac{1}{p} \sum_{j=1}^m \left ({\sum_{i=1}^p {\widetilde l^*_ {ij}}^4 - \frac{\left(\sum_{i = 1}^p {\widetilde l^*_ {ij}}^2 \right)^2}{p} }\right )$$

5. Factor Scores

Weighted Least Squares Method

  • Suppose that $\mu$, $L$, and $\psi$ are known.
  • Then $X-\mu = LF + \epsilon \sim \Pi_p(0, \psi)$

$$\hat F = (L’ \psi ^{-1}L)^{-1}L’ \psi^{-1} (X-\mu)$$

Regression Method

From the mean of the conditional distribution of $F|X$ is $\mu_{f|x} = L’(LL’+\psi)^{-1}(x-\mu)$

$$\hat F = \hat E(F|X) = L’\Sigma^{-1}(X-\overline X)$$